The sigmoid function is defined as:

sigmoid(x) = 1 / (1 + exp(-x))

where exp is the exponential function.

Properties of the Sigmoid Function

1. Range: The output of the sigmoid function always falls between 0 and 1.
2. Asymptotes: The function approaches 0 as x approaches negative infinity, and it approaches 1 as x approaches positive infinity.
3. Derivative: The derivative of the sigmoid function is given by:

sigmoid'(x) = sigmoid(x)(1 - sigmoid(x))

This derivative is important because it helps us update our model parameters during training.

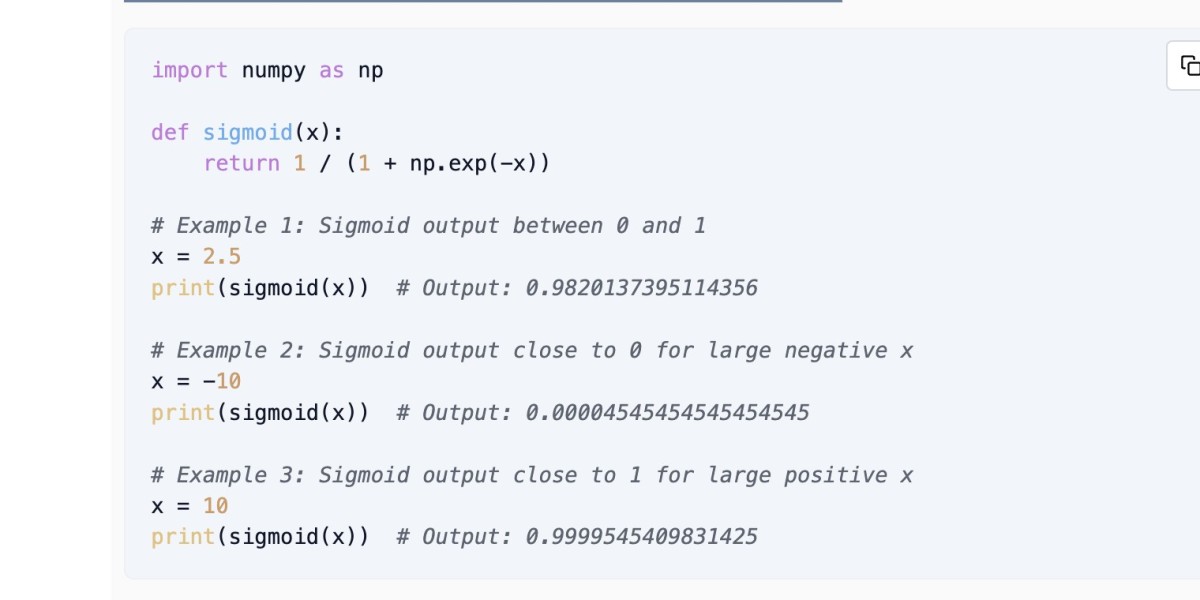
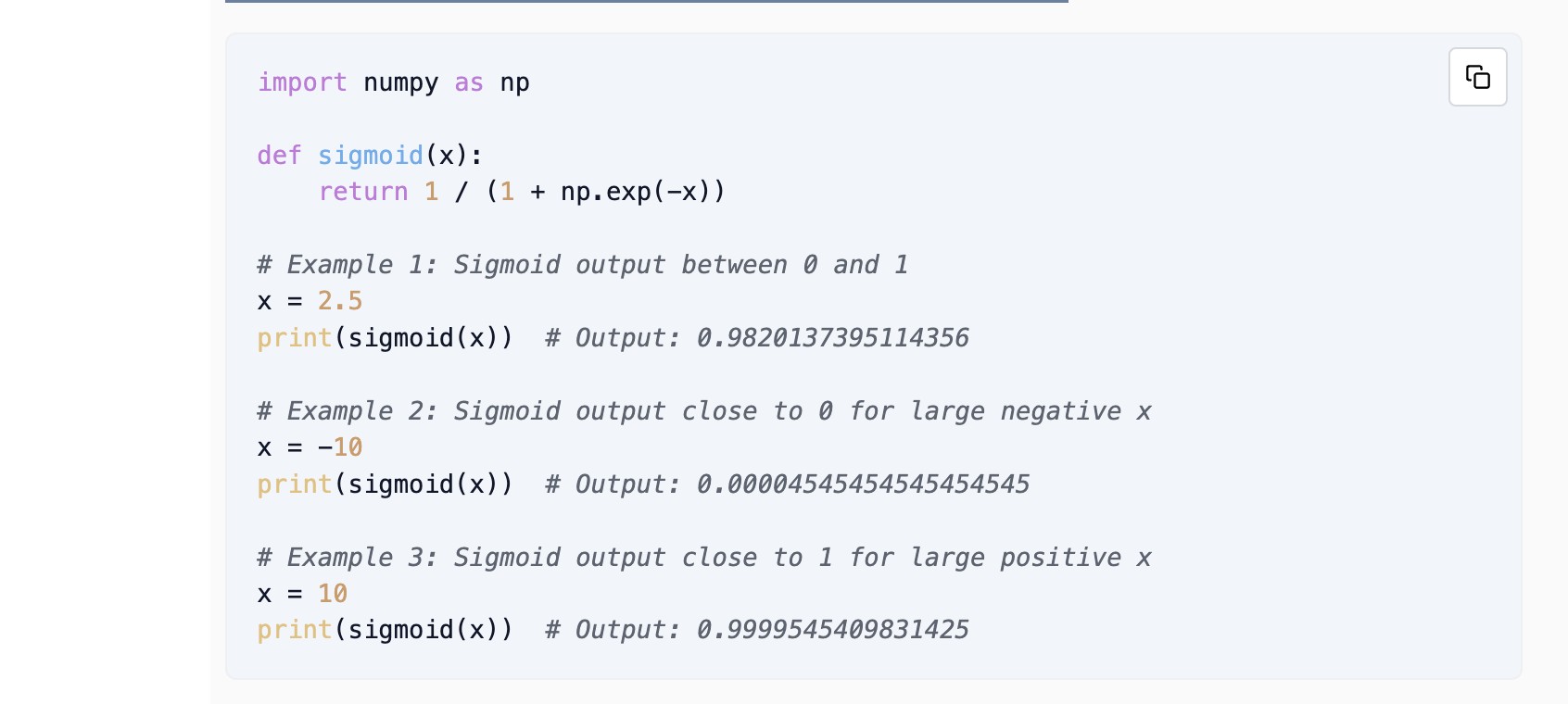
Examples in Code

Here are some examples of using the sigmoid function in code:

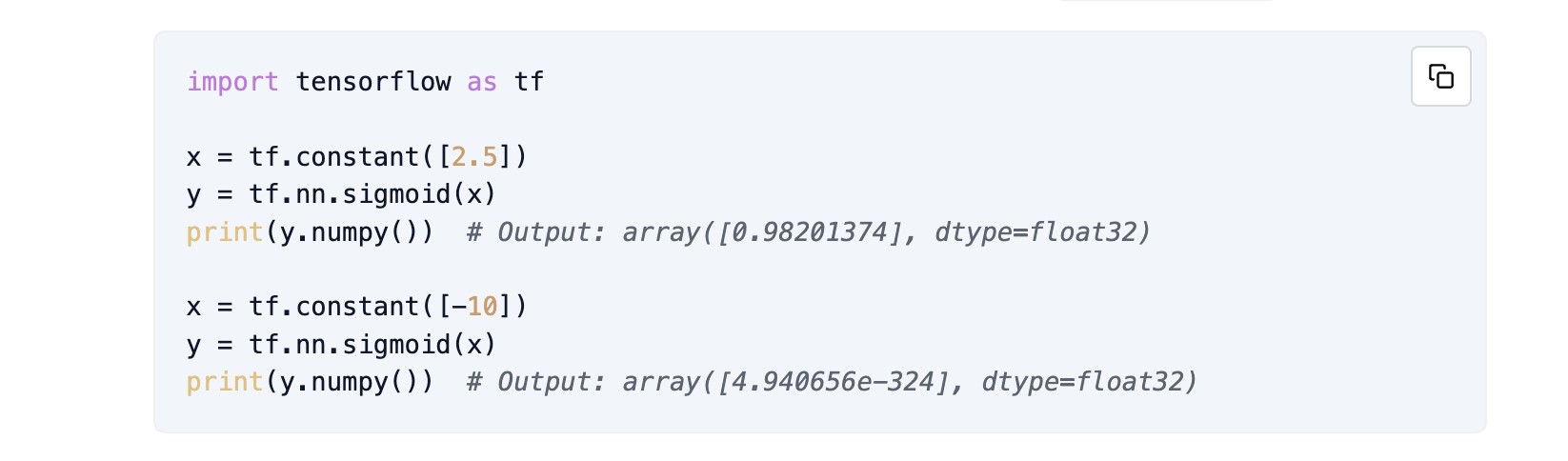
Implementing the Sigmoid Function in TensorFlow

In TensorFlow, you can implement the sigmoid function using the tf.nn.sigmoid function:

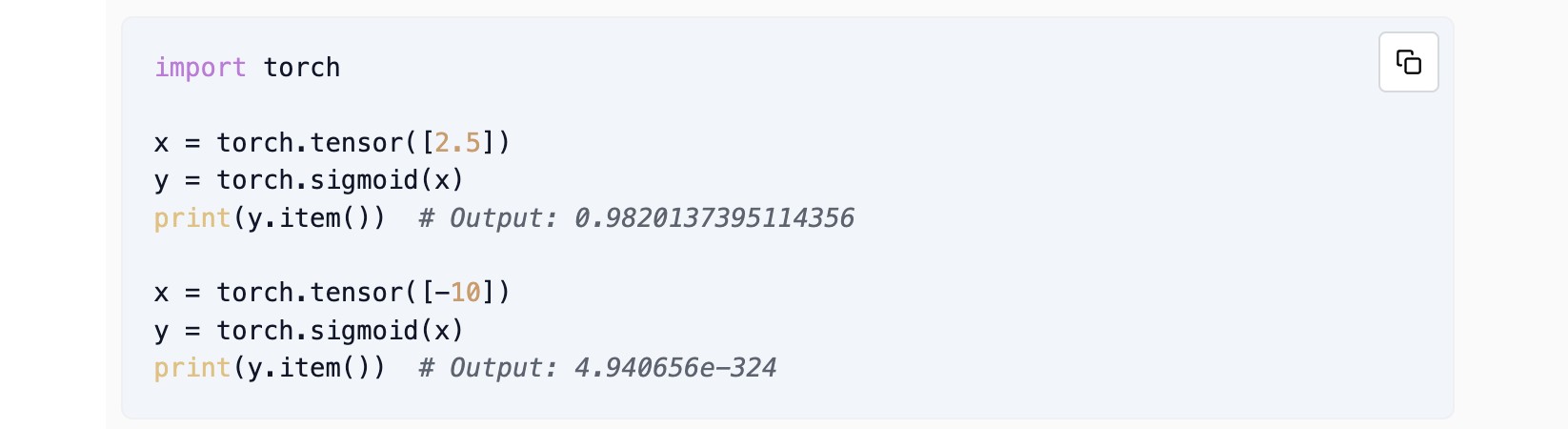
Implementing the Sigmoid Function in PyTorch

In PyTorch, you can implement the sigmoid function using the torch.sigmoid function:

I hope this helps you understand the sigmoid function better! Let me know if you have any further questions.